Τι; και σε σας συμβαίνει; τι μου λέτε; και θα έπαιρνα όρκο πως αποκλείεται.
Αν κάνουμε ένα γκάλοπ, αν κάνουμε μια μικρή έρευνα, θα δούμε πως όλοι λίγο πολύ συμφωνούν σε αυτό το φαινόμενο: όλων μας οι φίλοι έχουν περισσότερους φίλους από μας. Πριν μας τρελάνει για τα καλά αυτή η ιδέα, ας ανακουφιστούμε με το γεγονός ότι το φαινόμενο είναι παγκοσμίως παρατηρημένο και ονομάζεται το Παράδοξο της Φιλίας (Friendship Paradox).
Διότι πράγματι πρόκειται για παράδοξο: Πώς γίνεται όλοι οι φίλοι μας να έχουν περισσότερους φίλους… και ταυτόχρονα να βρίσκουν πως κι εκείνων οι φίλοι έχουν περισσότερους φίλους… άρα ποιος έχει περισσότερους φίλους; Και γιατί νομίζουμε πάντα πως είμαστε εμείς;

Μαντέψτε ποιος είναι ο πιο δημοφιλής.
Το φαινόμενο του Παραδόξου της Φιλίας παρατηρήθηκε σχετικά πρόσφατα, για πρώτη φορά από τον κοινωνιολόγο Scott L. Feld, το 1991. Σύμφωνα με αυτό, είναι γενική η παρατήρηση ότι καθένας μας έχει λιγότερους φίλους από τους φίλους του. Η διαπίστωση αυτή προήλθε από την μελέτη των κοινωνικών δικτύων. Ο Feld υπολόγισε τον μέσο όρο των φίλων που ένα άτομο έχει εντός ενός κοινωνικού δικτύου και τον συνέκρινε με τον μέσο όρο των φίλων που είχαν οι φίλοι του.
Αυτό που προέκυψε ήταν απρόβλεπτο και απολύτως παράλογο: Ο δεύτερος μέσος όρος, ασχέτως των επαναλήψεων, έβγαινε σταθερά μεγαλύτερος! Με άλλα λόγια: οι φίλοι μας πάντα έβγαιναν πιο δημοφιλείς από μας.
Είναι ενδιαφέρον να παρατηρήσουμε την εφαρμογή του Παράδοξου της Φιλίας και στα διαδικτυακά κοινωνικά δίκτυα (μάλιστα, εκεί η διαπίστωση είναι ακόμα εμφανέστερη, καθώς μιλάμε με εύκολα διακριτά νούμερα): στο Facebook, οι φίλοι μου έχουν περισσότερους φίλους – στο Twitter, οι followers μου έχουν περισσότερους followers από μένα. Ακόμα και στις διαπροσωπικές σχέσεις, όμως, οι ερωτικοί μου σύντροφοι τείνουν να έχουν περισσότερους ερωτικούς συντρόφους από ό,τι εγώ.
Ας επιστρέψουμε για λίγο στον Feld. Ο Feld λοιπόν υποστηρίζει ότι το φαινόμενο αυτό μπορεί να εξηγηθεί ως μια μορφή δειγματοληπτικού θορύβου, κατά τον οποίο οι άνθρωποι με μεγαλύτερο αριθμό φίλων έχουν αυξημένη πιθανότητα να βρεθούν φίλοι κάποιου τρίτου ατόμου. Με τον όρο «δειγματοληπτικός θόρυβος» περιγράφεται το «θάμπωμα» της επιλογής των σωστών επιλογών μέσου όρου λόγω εξωγενών παραγόντων όπως κοινωνία, στερεότυπα κ.ο.κ., όπως θα δούμε παρακάτω. Την παράδοξη φύση του φαινομένου εξήγησε σαν συνέπεια των γενικών μαθηματικών ιδιοτήτων των κοινωνικών δικτύων. Τα μαθηματικά του παραδόξου σχετίζονται άμεσα με την αριθμο-γεωμετρική μέση ανισότητα και την ανισότητα Cauchy-Schwarz. Για να μη σας μπλέξω με μαθηματικές εξισώσεις και χάσω κι άλλους φίλους, θα προσπαθήσω να σας το εξηγήσω σχηματικά.

Για τις ανάγκες του παραδείγματος, η Ana έγινε Μαρία, ο Bill Κώστας, η Carla Αργυρώ και ο Dan Ηλίας (βλ.παρακάτω)
Ο φίλος μας ο Feld λοιπόν ορίζει την φιλία ως συμμετρική σχέση και την απεικονίζει με τη μορφή ενός τριγώνου. Αν στις τρεις γωνίες του τριγώνου βάλουμε τρία άτομα (πχ Τη Μαρία, τον Κώστα και την Αργυρώ), τότε συμβαίνει το εξής παράδοξο: ενώ η Μαρία έχει φίλους και τον Κώστα και την Αργυρώ, τείνει να χρησιμοποιεί σαν παράδειγμα σύγκρισης τον Κώστα που είναι γενικά πιο ανοιχτός στο να κάνει φίλους, παρά την Αργυρώ, που είναι πιο μοναχική. Γιατί; Διότι τείνουμε να θεωρούμε το «καλύτερο» ως κανόνα και το «λιγότερο καλό» ως εξαίρεση. Το πρόβλημα έγκειται στο ότι ο Κώστας μας έκανε φίλους επειδή είναι δημοφιλής, άρα το να χρησιμοποιούμε αυτόν σαν μέτρο σύγκρισης, είναι εξ ορισμού εγγύηση ότι θα μας βγάλει το συμπέρασμα πως είμαστε λιγότερο δημοφιλείς… πόσο μάλλον που, στο τρίγωνο, ο Κώστας έχει φίλη και την Αργυρώ (η οποία όμως στη διαδικασία μας μετράει ως εξαίρεση, άρα δεν την υπολογίζουμε στην σύγκριση – πράγμα που μας ζημιώνει, γιατί στο τρίγωνο έχουμε όλοι, τελικά, τους ίδιους φίλους!). Τα άτομα με τα οποία τείνουμε να συγκρινόμαστε είναι πιο «κεντρικής» σημασίας στον κοινωνικό μας περίγυρο, άρα και πιο πιθανό να είναι όντως πιο δημοφιλή – είναι όμως ο μέσος όρος;
Ας επιστρέψουμε στο διαδίκτυο, που τα πράγματα είναι πιο ξεκάθαρα. Στο Twitter, οι άνθρωποι των οποίων είμαστε followers είναι μάλλον αρκετά δημοφιλείς, άρα εμείς κάνουμε follow σε άτομα πιο δημοφιλή και μας κάνουν follow άτομα λιγότερο δημοφιλή από μας – σκεφτείτε το σαν μια πυραμίδα δημοφιλίας. Κοιτάμε μόνιμα προς τα πάνω όταν συγκρίνουμε. Ωστόσο, ο μέσος όρος δεν βρίσκεται εκεί.
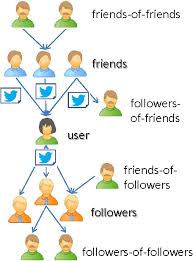
Ένα μικρό διαδικτυακό σχήμα.
Ένα παράδειγμα που μπορεί να βοηθήσει, είναι αν φανταστούμε τον εαυτό μας σε ένα πάρτι γεμάτο διασημότητες. Εμείς αντιλαμβανόμαστε τον εαυτό μας σαν μέσο όρο ανθρώπου, οπότε αναπόφευκτα συγκρινόμαστε σαν μέσος όρος με τους άλλους. Στο πάρτι αυτό όμως, παιδιά, ας μη γελιόμαστε: δεν είμαστε ο μέσος όρος. Άρα, αν βρούμε όλους τους υπολοίπους πιο διάσημους από εμάς, δεν ισχύει: εμείς είμαστε σε αυτήν την χωροχρονική στιγμή το ξένο σώμα, η εξαίρεση. Εμείς είμαστε κατ’ εξαίρεση οι λιγότερο διάσημοι.
Να κι ένα παράδειγμα πιο συγκεκριμένο και περισσότερο σχηματικό:
Ας χρησιμοποιήσουμε ξανά τη Μαρία, τον Κώστα και την Αργυρώ, μια χαρά παιδιά είναι, και μας βοήθησαν αρκετά στο προηγούμενο παράδειγμα. Όμως τώρα θα προσθέσουμε και τον Ηλία. Το σχήμα μας έχει ως εξής:
- Η Μαρία και ο Κώστας είναι φίλοι μεταξύ τους
- Ο Κώστας είναι φίλος με όλους
- Η Αργυρώ είναι φίλη με τον Κώστα και τον Ηλία
- Ο Ηλίας είναι φίλος με τον Κώστα και την Αργυρώ.
Κατά συνέπεια : η Μαρία έχει ένα φίλο, ο Κώστας 3, και η Αργυρώ και ο Ηλίας έχει καθένας από 2.
Ας δούμε τώρα πόσους φίλους φίλων έχει ο καθένας.
Η Μαρία είναι φίλη με τον Κώστα που έχει 3 φίλους. Ο Κώστας είναι φίλος με όλους, άρα διαθέτει 5 φίλους φίλων. Επίσης, η Αργυρώ και ο Ηλίας έχουν 5 φίλους φίλων ο καθένας. Είναι φυσικό λοιπόν για τον Κώστα να έχει τους λιγότερους φίλους φίλων, και τους περισσότερους δικούς του φίλους, καθώς είναι πολύ δημοφιλής, το είπαμε και νωρίτερα . Δεν μας προκαλεί δα και καμία έκπληξη ότι ένας δημοφιλής άνθρωπος έχει περισσότερους φίλους από τους φίλους του. Άρα, πού είναι το παράδοξο που λέγαμε τόσην ώρα;
Το παράδοξο έρχεται όταν κάνουμε τις μαθηματικές πράξεις. Τόσην ώρα μιλάμε για 4 άτομα, άρα οι σχέσεις φτάνουν τις 8: αυτό σημαίνει πως ο μέσος όρος φίλων τους είναι 2 φίλοι.
Από την άλλη, μέσα στα 4 άτομα βρήκαμε 18 φίλους φίλων: αυτό σημαίνει ότι ο μέσος φίλος μας έχει 2,25 φίλους. 0,25 φίλους παραπάνω από όσους έχουμε εμείς!
Με λίγα λόγια, το Παράδοξο της Φιλίας προκύπτει από το γεγονός ότι αλλιώς υπολογίζω τον μέσο όρο για μένα κι αλλιώς για τους φίλους μου.
Οι ερευνητές προσπάθησαν να δώσουν ένα ακόμη παράδειγμα, εφαρμόζοντας το φαινόμενο αυτό με την… γρίπη.
Το Εθνικό Σύστημα Υγείας ποθεί να εμβολιάσει όλους τους ανθρώπους στον κόσμο, ώστε να μειωθεί η εξάπλωση του ιού της γρίπης. Ξέρουμε βέβαια πως αυτό δεν είναι εφικτό. Έτσι, εναλλακτικά, επιλέγει να εμβολιάσει τους ανθρώπους που είναι περισσότερο πιθανό να διαδώσουν τον ιό: τους κοινωνικούς ανθρώπους, με ευρύ φιλικό κύκλο. Αυτό σημαίνει πως ιδανικά θα έπρεπε να φτιάξουμε ένα σχεδιάγραμμα που θα μας αποκάλυπτε τον ιδανικό κοινωνικό υποψήφιο. Κάτι τέτοιο όμως βέβαια θα ήταν και χρονοβόρο και δαπανηρό.

Παρότρυνση προς τους δημοφιλείς.
Έτσι, αποφάσισαν να ακολουθήσουν μια συντομότερη οδό:
Αρχικά, πήραν ένα τυχαίο δείγμα ανθρώπων και τους ζήτησαν να ονομάσουν έναν φίλο. Οι πιθανότητες να αναφέρουν έναν μοναχικό και απομακρυσμένο φίλο ήταν πολύ λίγες: το λογικό είναι να αναφέρουν το όνομα του πιο κοινωνικού τους φίλου, του καλύτερου, του πιο δημοφιλή (του Κώστα). Έτσι λοιπόν, βασιζόμενοι στο Παράδοξο της Φιλίας έκριναν πως αυτός θα ήταν ο πλέον δημοφιλής, άρα και ο πιο κοινωνικός, άρα και ο πιο πιθανός να μεταδώσει την ασθένεια, άρα, Κωστάκη, ετοιμάσου για το εμβόλιο!
Εξ αποτελέσματος, οι ερευνητές διαπίστωσαν ότι πράγματι τα συγκεκριμένα δημοφιλή άτομα που είχαν ήδη εντοπίσει με αυτήν την μέθοδο ήταν και τα πρώτα που κόλλησαν την γρίπη.
Συμπέρασμα: Οι φίλοι σας μπορεί να είναι πιο δημοφιλείς από σας, αλλά αν εμβολιαστούν σας γλιτώνουν από διάφορες επιδημίες.
***
της Βυζαντίας Πυριόχου-Γκυ
Πηγή: reasonmachine
Αντικλείδι , https://antikleidi.com