
Βρίσκεστε σε ένα τηλεπαιχνίδι στην τηλεόραση. Στο τηλεπαιχνίδι αυτό ο στόχος σας είναι να κερδίσετε το έπαθλο, που είναι ένα αυτοκίνητο. Ο παρουσιαστής του τηλεπαιχνιδιού σας δείχνει τρεις πόρτες. Λέει πως πίσω από την μία υπάρχει και πίσω από τις άλλες, δύο κατσίκες. Σας ζητάει να διαλέξετε μια πόρτα. Εσείς διαλέγετε μία πόρτα αλλά η πόρτα δεν ανοίγει. Ύστερα ο παρουσιαστής ανοίγει μια από τις πόρτες που δεν διαλέξατε και σας δείχνει μία κατσίκα(γιατί αυτός ξέρει τι υπάρχει πίσω από τις πόρτες). Ύστερα λέει πως έχετε μία τελευταία ευκαιρία ν’ αλλάξετε γνώμη προτού ανοίξουν οι πόρτες και σας τύχει ένα αυτοκίνητο ή μία κατσίκα. Σας ρωτάει λοιπόν αν θέλετε να αλλάξετε γνώμη και να διαλέξετε την άλλη κλειστή πόρτα. Τι πρέπει να κάνετε;
Η Μέριλιν Σέιβαντ απάντησε πως πρέπει να αλλάξετε γνώμη και να διαλέξετε την τελική πόρτα, γιατί οι πιθανότητες είναι 2 προς 3 ότι πίσω από εκείνη την πόρτα θα υπάρχει ένα αυτοκίνητο.
Αν όμως χρησιμοποιήσετε την διαίσθησή σας, φαντάζεστε πως οι πιθανότητες είναι 50:50, γιατί πιστεύετε πως μπορεί πράγματι να είναι πίσω από οποιαδήποτε πόρτα.
Πολλοί άνθρωποι έγραψαν στο περιοδικό για να πουν ότι η Μέριλιν έκανε λάθος, ακόμα και όταν εκείνη εξήγησε πολύ προσεκτικά το γιατί είχε δίκιο. Το 92% της αλληλογραφίας που έλαβε σχετικά με το πρόβλημα έλεγε πως έκανε λάθος και πολλά από αυτά τα γράμματα προέρχονταν από μαθηματικούς και επιστήμονες. Αναφέρω ενδεικτικά κάποια από τα γράμματα που έλαβε:
Ανησυχώ πολύ με την γενική έλλειψη μαθηματικών ικανοτήτων από τους αναγνώστες σας. Παρακαλώ να βοηθήσετε ομολογώντας το σφάλμα σας. Δρ Ρόμπερτ Σάκς, Πανεπιστήμιο Τζορτζ Μέισον
Υπάρχει αρκετός μαθηματικός αναλφαβητισμός σε τούτη την χώρα και δεν χρειάζεται να τον αυξάνει ακόμα περισσότερο το άτομο με τον υψηλότερο δείκτη νοημοσύνης στον κόσμο. Ντροπή! Δρ Σκοτ Σμιθ, Πανεπιστήμιο της Φλόριντα
Έχω σοκαριστεί από το γεγονός ότι, αφού σας διόρθωσαν τουλάχιστον τρείς μαθηματικοί εξακολουθείτε να μην βλέπετε το λάθος σας. Κεντ Φορντ, Κρατικό Πανεπιστήμιο Ντίκινσον
Είμαι σίγουρος ότι θα λάβατε πολλές επιστολές από μαθητές λυκείου και φοιτητές. Ίσως θα έπρεπε να κρατήσετε μερικές διευθύνσεις για να σας βοηθήσουν σε μελλοντικά σας άρθρα. Δρ Ο. Ρόμπερτ Σμιθ, Κρατικό Πανεπιστήμιο της Τζόρτζια
Κάνετε εντελώς λάθος… Πόσοι εξοργισμένοι μαθηματικοί χρειάζονται για να σας αλλάξουν τα μυαλά; Δρ Ε. Ρέι Μπόμπο, Πανεπιστήμιο Τζορτζτάουν
Αν όλοι αυτοί οι δόκτορες έκαναν λάθος, η χώρα μας θα βρισκόταν σε πολύ δεινή θέση. Δρ Έβερτ Χάρμαν, Αμερικανικό Ινστιτούτο Στρατιωτικών Ερευνών
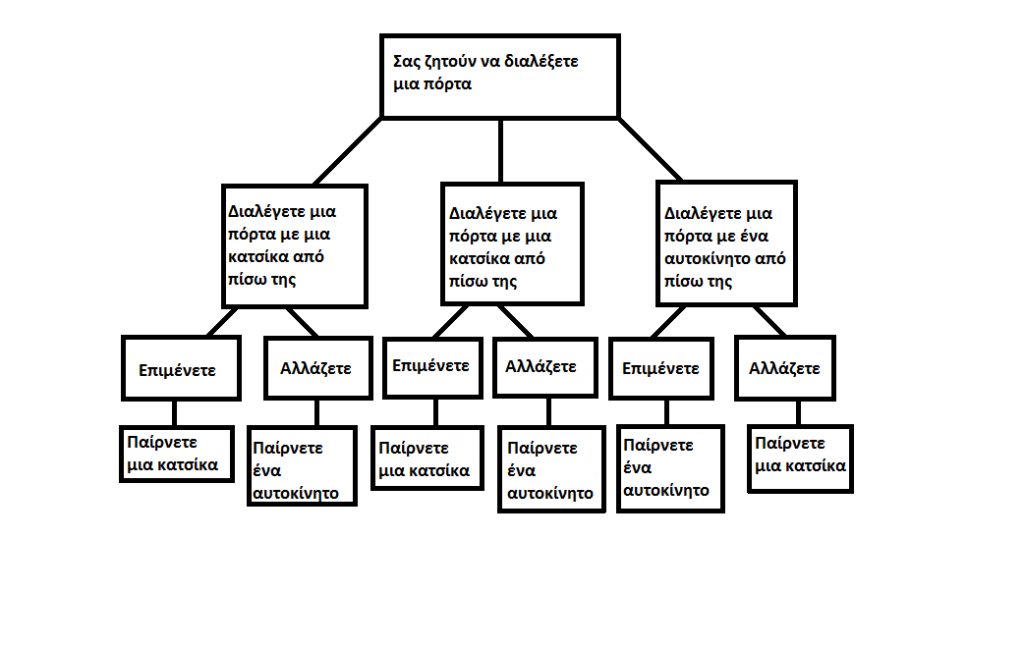
Όμως η Μέριλιν Σέιβαντ είχε δίκιο. Και ιδού o τρόπος με τον οποίο μπορείτε να το αποδείξετε εξετάζοντας τις πιθανότητες νίκης επιμένοντας στην αρχική σας επιλογή ή αλλάζοντας γνώμη:
Επιμένοντας
Αν επιμείνετε στην αρχική σας απόφαση η πιθανότητα να κερδίσετε μια κατσίκα είναι 2/3 αφού οι κατσίκες είναι δύο και οι πόρτες τρείς. Έτσι οι πιθανότητες να κερδίσετε το αυτοκίνητο είναι 1/3. Γι’ αυτό σίγουρα δεν συμφέρει να επιμείνετε στην αρχική σας απόφαση.
Αλλάζοντας γνώμη
Εξετάζοντας το φαινόμενο να αλλάξετε γνώμη καταλήγουμε ότι: Οι πιθανότητες να έχετε αρχικά επιλέξει την κατσίκα είναι 2/3 και βλέποντας την κατσίκα από την ανοιχτή πόρτα αλλάζετε στην τελευταία και κερδίζετε το αυτοκίνητο. Ενώ αντίθετα οι πιθανότητες να έχετε επιλέξει αρχικά το αυτοκίνητο και αλλάζοντας να πάρετε την κατσίκα είναι 1/3.
______
Πηγές: απόσπασμα από το βιβλίο ΠΟΙΟΣ ΣΚΟΤΩΣΕ ΤΟΝ ΣΚΥΛΟ ΤΑ ΜΕΣΑΝΥΧΤΑ, Μαρκ Χάντον
To είδαμε εδώ: http://acstec.wordpress.com/
“Παίξτε” κι εσείς εδώ : http://www.math.ucsd.edu/
Αντικλείδι , https://antikleidi.com
Συναφές:
Το παράδοξο των γενεθλίων και πόσο κακοί είμαστε στην εκτίμηση του ρίσκου
Πως μπορείτε να γίνετε ειδήμων σε οτιδήποτε
Τα 10 πιο όμορφα πειράματα φυσικής
10 όρια στην ανθρώπινη αντίληψη … και πώς αυτά διαμορφώνουν τον κόσμο μας





Λυπάμαι που σας το χαλάω παιδιά, αλλά η Μέριλιν έχει λάθος.
Το λάθος βρίσκεται στο ότι συνεχίζει να δίνει 33% πιθανότητα στο αυτοκίνητο, ακόμα κι όταν έχει ανοίξει μία κουρτίνα.
Συγκεκριμένα, πριν το άνοιγμα της κουρτίνας, η πιθανότητα να βρίσκεται το αυτοκίνητο πίσω από οποιαδήποτε από αυτές είναι 33%. 33% η πιθανότητα να βρίσκεται πίσω από την 1η κουρτίνα, 33% να βρίσκεται πίσω από τη 2η, και 33% να βρίσκεται πίσω από την 3η.
Μετά το άνοιγμα όμως της κουρτίνας (πίσω από την οποία υπάρχει κατσίκα), τα δεδομένα άλλαξαν. Η πιθανότητα πλέον να βρίσκεται το αυτοκίνητο πίσω από την ανοιγμένη κουρτίνα είναι 0% (αφού το γνωρίζουμε ότι υπάρχει κατσίκα εκεί). Και επομένως, η πιθανότητα να βρίσκεται σε οποιαδήποτε από τις άλλες δύο, είναι 50%. 50% να βρίσκεται πίσω από την 1η κλειστή κουρτίνα, και 50% να βρίσκεται πίσω από τη 2η κλειστή κουρτίνα.
Άρα, είτε αλλάξει γνώμη ο παίκτης, είτε όχι, είναι το ίδιο και το αυτό.
Γενικά, μετά το άνοιγμα της κουρτίνας, το παιχνίδι άλλαξε.
Δεν έχουμε πλέον 3 κουρτίνες, 2 κατσίκες και 1 αυτοκίνητο.
Έχουμε 2 κουρτίνες, 1 κατσίκα και 1 αυτοκίνητο.
Και το 50-50 δεν είναι απλώς διαίσθηση. Είναι μαθηματικά.
Ουπς! Κατά λάθος έστειλα την απάντηση δύο φορές.
Επίσης, πρόκειται για πόρτες και όχι για κουρτίνες.
Τελικά, όταν ξεχνάς το ρητό: “Μη κρίνετε, ίνα μη κριθήτε”, πρέπει να υποστείς και τις συνέπειες.
Λυπάμαι που σας το χαλάω παιδιά, αλλά η Μέριλιν έχει λάθος. Το λάθος βρίσκεται στο ότι συνεχίζει να δίνει 33% πιθανότητα στο αυτοκίνητο, ακόμα κι όταν έχει ανοίξει μία κουρτίνα.
Συγκεκριμένα, πριν το άνοιγμα της κουρτίνας, η πιθανότητα να βρίσκεται το αυτοκίνητο πίσω από οποιαδήποτε από αυτές είναι 33%. 33% η πιθανότητα να βρίσκεται πίσω από την 1η κουρτίνα, 33% να βρίσκεται πίσω από τη 2η, και 33% να βρίσκεται πίσω από την 3η.
Μετά το άνοιγμα, όμως, της κουρτίνας (πίσω από την οποία υπάρχει κατσίκα), τα δεδομένα άλλαξαν. Η πιθανότητα πλέον να βρίσκεται το αυτοκίνητο πίσω από την ανοιγμένη κουρτίνα είναι 0% (αφού το γνωρίζουμε ότι υπάρχει κατσίκα εκεί). Και επομένως, η πιθανότητα να βρίσκεται σε οποιαδήποτε από τις άλλες δύο είναι 50%. 50% να βρίσκεται πίσω από την 1η κλειστή κουρτίνα, και 50% να βρίσκεται πίσω από τη 2η κλειστή κουρτίνα.
Άρα, είτε αλλάξει γνώμη ο παίκτης, είτε όχι, είναι το ίδιο και το αυτό.
Γενικά, μετά το άνοιγμα της κουρτίνας, το παιχνίδι άλλαξε.
Δεν έχουμε πλέον 3 κουρτίνες, 2 κατσίκες και 1 αυτοκίνητο.
Έχουμε 2 κουρτίνες, 1 κατσίκα και 1 αυτοκίνητο.
Και το 50-50 δεν είναι απλώς διαίσθηση. Είναι μαθηματικά.
Φυσικά και πρέπει να αλλάξει την πόρτα. Την καλύτερη εξήγηση τη διάβασα στο βιβλίο ο γρίφος της Σεχραζάντ. Όταν οι κουρτίνες είναι μόλις τρεις η διαφορά μεταξύ των πιθανοτήτων είναι πολύ μικρή (66% με 50%). Σκεφτείτε όμως πως οι κουρτίνες είναι 10. Διαλέγει ο παίχτης τον αριθμό 1. Ο παρουσιαστής ενώ ξέρει που βρίσκεται το δώρο, και εδώ είναι όλη η ουσία του πειράματος, ανοίγει τις υπόλοιπες που είναι κενές και αφήνει την 10. Ξεπερνάμε το γεγονός πως ο παρουσιαστής μπορεί να μπλοφάρει καθώς μιλάμε για καθαρά μαθηματικά.Σε αυτή την περίπτωση αν ο παίχτης διαλέξει την κουρτίνα 10 η πιθανότητα είναι 50%; Δεν νομίζω. Για την ακρίβεια είναι 90%. Δεσμευμένες πιθανότητες για όσους ξέρουν.